Design of TensorFlow XLA Sharding System

Posted on Last updated on

Recently, a SOTA sharding approach, GSPMD/GShard, was proposed and it provides an intuitive interface to partition a large array on arbitrary dimensions, while utilizing sharding propagation algorithms to automatically infer the partitioning strategy for tensors without user-specified sharding specifications. This document introduces the design and the implementation of XLA Sharding System.

upload successful
upload successful

HloSharding Object

First of all, we need a way to represent sharding specifications using programming language. XLA designed an object to do such a thing, and this object contains numerous variables and a set of supporting functions to configure itself. Some attributes of HloSharding are listed below.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// File: tensorflow/compiler/xla/service/hlo_sharding.h

class HloSharding {
  bool replicated_;
  bool maximal_;
  bool tuple_;
  bool manual_;
  // This field is only used if replicated_ is false. If maximal_ is true, then
  // the field contains a rank 1 array with a single element, which is the
  // device the HLO is assigned to. If maximal_ is false, the field contains an
  // array with the same rank as the corresponding HLO. The dimension sizes of
  // the array describe the number of ways the HLO is partitioned along each
  // dimension. The values of the array specify which device each tile of
  // the HLO is assigned to. The index of each value determines which tile it
  // takes.
  // For example, {{{2, 3}}, {{5, 7}}} (whose ToString representation is
  // "{devices=[2,1,2]2,3,5,7}"), means that dimension 1 is split two way and
  // dimension 3 is split 2 way. Core 5, whose index is [2,1,1] will take the
  // tile that contains the 2nd half of dimension 1 and the 1st half of
  // dimension 3.
  Array<int64> tile_assignment_;
  // Only non-empty when tuple_ is true. If a tuple is empty then one entry is
  // present for the root. This is a flattened list of all the leaf shardings in
  // a tuple shape, by pre-order walk (ShapeTree iterator order).
  std::vector<HloSharding> tuple_elements_;
  // This flag is to support partial replication and partial sharding. If it is
  // true, tile_assignment_ will have an extra dimension in addition to the data
  // shape rank, and the added last dimension represents the subgroups of
  // replications, i.e., elements in slice [..., :] will be replicated.
  bool replicate_on_last_tile_dim_;
  // This field is used to track the source of this sharding, usually derived
  // from instructions. Multiple metadata may be populated if sharding is
  // combined with other shardings. Metadata are to not be populated when
  // tuple_ == true and instead metadata should be set on individual tuple
  // elements.
  std::vector<OpMetadata> metadata_;
};

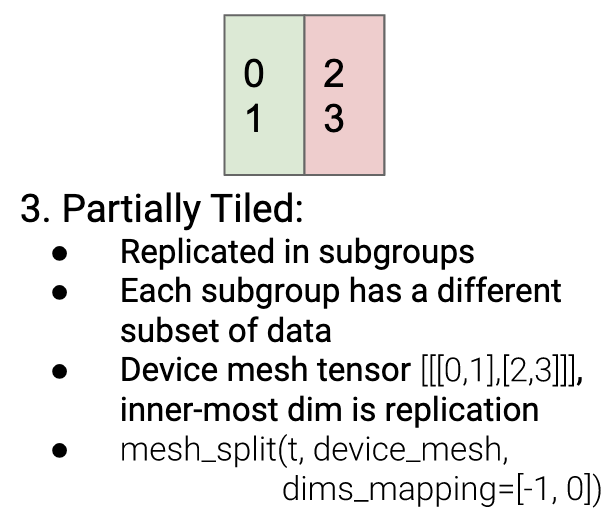
Array<int64> tile_assignment_ here is multi-dimensional with arbitrary shape. {devices=[2,1,2]2,3,5,7} means the shape of tile_assignment_ is [2,1,2], while the values are {2,3,5,7}.

std::vector<HloSharding> tuple_elements_ probably was designed to specify the sharding specifications of outputs.

I am not aware of what the roles of maximal_, tuple_elements_ are. Is there any body know that?

Note that each single object could be shared by multiple instructions. By doing this, the cost of creating and maintaining several instances with the exact same contents could be eliminated.

Extended HLO IR Attribute

The original implementation of XLA added the attribute std::shared_ptr<const HloSharding> sharding_ to the class xla::HloInstruction, which is declared in tensorflow/compiler/xla/service/hlo_instruction.h. A common usage of this HLO Instruction Attribute is to declare sharded tensors. Here is a sample HLO IR code with sharding attributes. Note that the Propagation Algorithm may fill in this attribute for those instructions without it.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
primitive_computation_add.6 {
  parameter.7 = f32[] parameter(0)
  parameter.8 = f32[] parameter(1)
  ROOT add.9 = f32[] add(parameter.7, parameter.8)
}

ENTRY xmap__lambda_.12 {
  constant.2 = pred[] constant(false)
  parameter.1 = f32[8]{0} parameter(0), parameter_replication={false}, sharding={replicated}
  custom-call.3 = f32[8]{0} custom-call(parameter.1), custom_call_target="Sharding", sharding={devices=[4]0,1,2,3}
  sine.4 = f32[8]{0} sine(custom-call.3)
  constant.5 = f32[] constant(0)
  reduce.10 = f32[] reduce(sine.4, constant.5), dimensions={0}, to_apply=primitive_computation_add.6
  ROOT tuple.11 = (f32[]) tuple(reduce.10), sharding={{replicated}}
}

Note: this HLO IR code is compiled from this JAX Frontend code

1
2
3
4
5
6
7
@jtu.with_mesh([('x', 4)])
def test():
    f = pjit(lambda x: jnp.sin(x).sum(),
             in_axis_resources=(P('x'),),
             out_axis_resources=None)
    x = jnp.arange(8, dtype=jnp.float32)
    f(x)

This example illustrates a lambda function takes a replicated tensor as the input, and splits this tensor by invoking custom-call, then performs the calculation.

SPMD Partitioner

You might notice that in the previous example, the instructions invoking operators (e.g. reduce.10) don’t contain sharding attributes. That leads to a critical question, how a regular operator reacts to sharded tensors. The solution of XLA is introducing SPMD Partitioner, which is mainly responsible for converting a full-sized operator into a partition-sized operator by adding necessary collective communication primitives to lower-layer IR code, and the partitioner also converts the inputs of operators from global tensor symbols with sharding to local tensor symbols without sharding specifications.

We could find some clues in tensorflow/compiler/xla/service/spmd/spmd_partitioner_test.cc.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
TEST_F(SpmdPartitioningTest, DotPartialContracting2) {
  absl::string_view hlo_string = R"(
HloModule module

ENTRY entry {
  %lhs = f32[24,100] parameter(0),
    sharding={devices=[1,2,2]0,1,2,3 last_tile_dim_replicate}
  %rhs = f32[32,100] parameter(1),
    sharding={devices=[1,2,2]0,1,2,3 last_tile_dim_replicate}
  ROOT %dot = f32[24,32] dot(%lhs, %rhs),
    lhs_batch_dims={}, rhs_batch_dims={},
    lhs_contracting_dims={1}, rhs_contracting_dims={1},
    sharding={devices=[2,1,2]0,2,1,3 last_tile_dim_replicate}
})";

  TF_ASSERT_OK_AND_ASSIGN(auto module,
                          PartitionComputation(hlo_string, /*num_devices=*/4));
  VLOG(1) << module->ToString();

  auto lhs = AllOf(op::Shape("f32[24,50]"), op::Parameter(0));
  auto rhs = AllOf(op::Shape("f32[32,50]"), op::Parameter(1));
  auto dot =
      AllOf(op::Shape("f32[12,32]"),
            op::Dot(AllOf(op::Shape("f32[12,50]"), op::DynamicSlice(lhs, _, _)),
                    rhs));
  auto root = module->entry_computation()->root_instruction();
  EXPECT_THAT(root, op::AllReduce(dot));
}

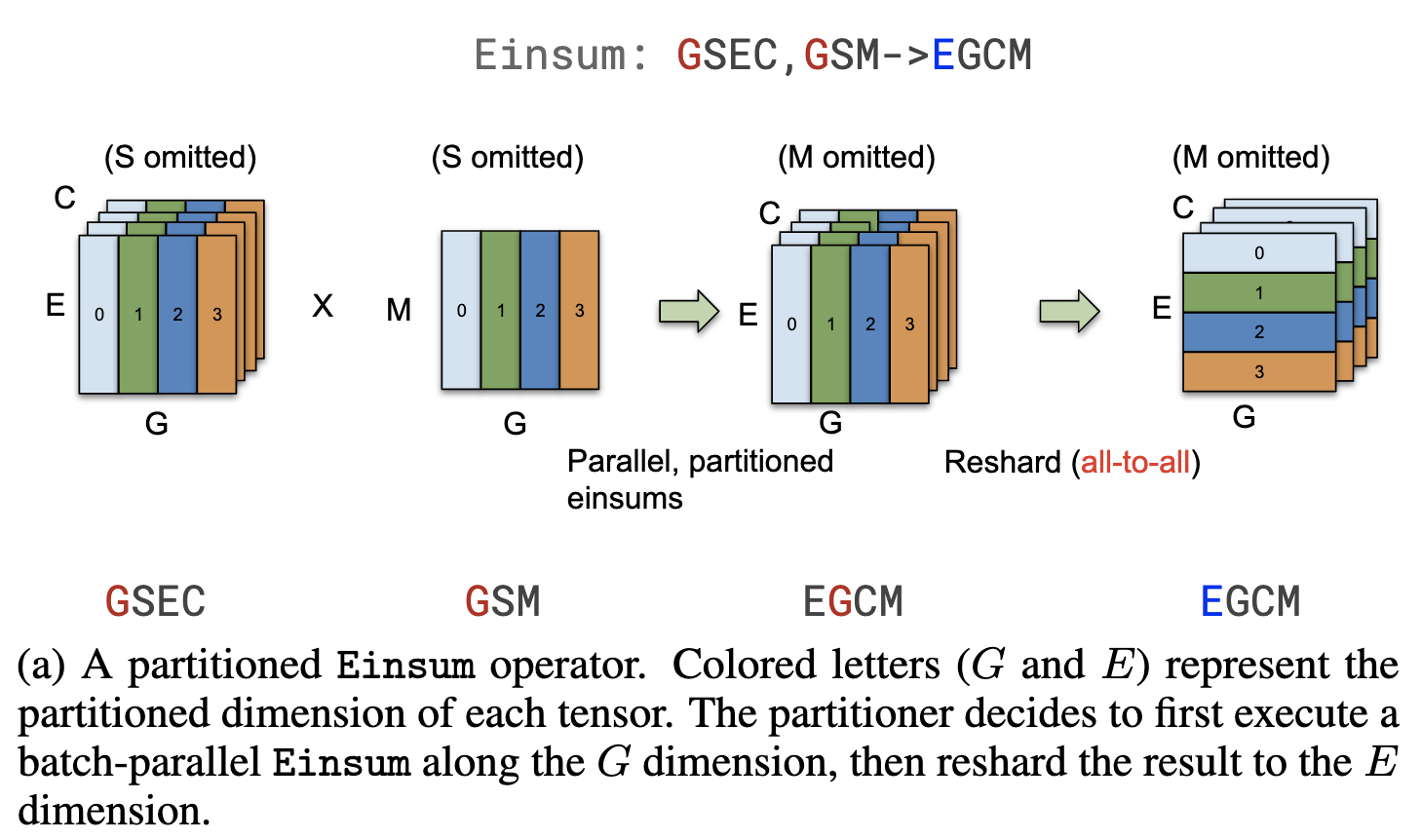
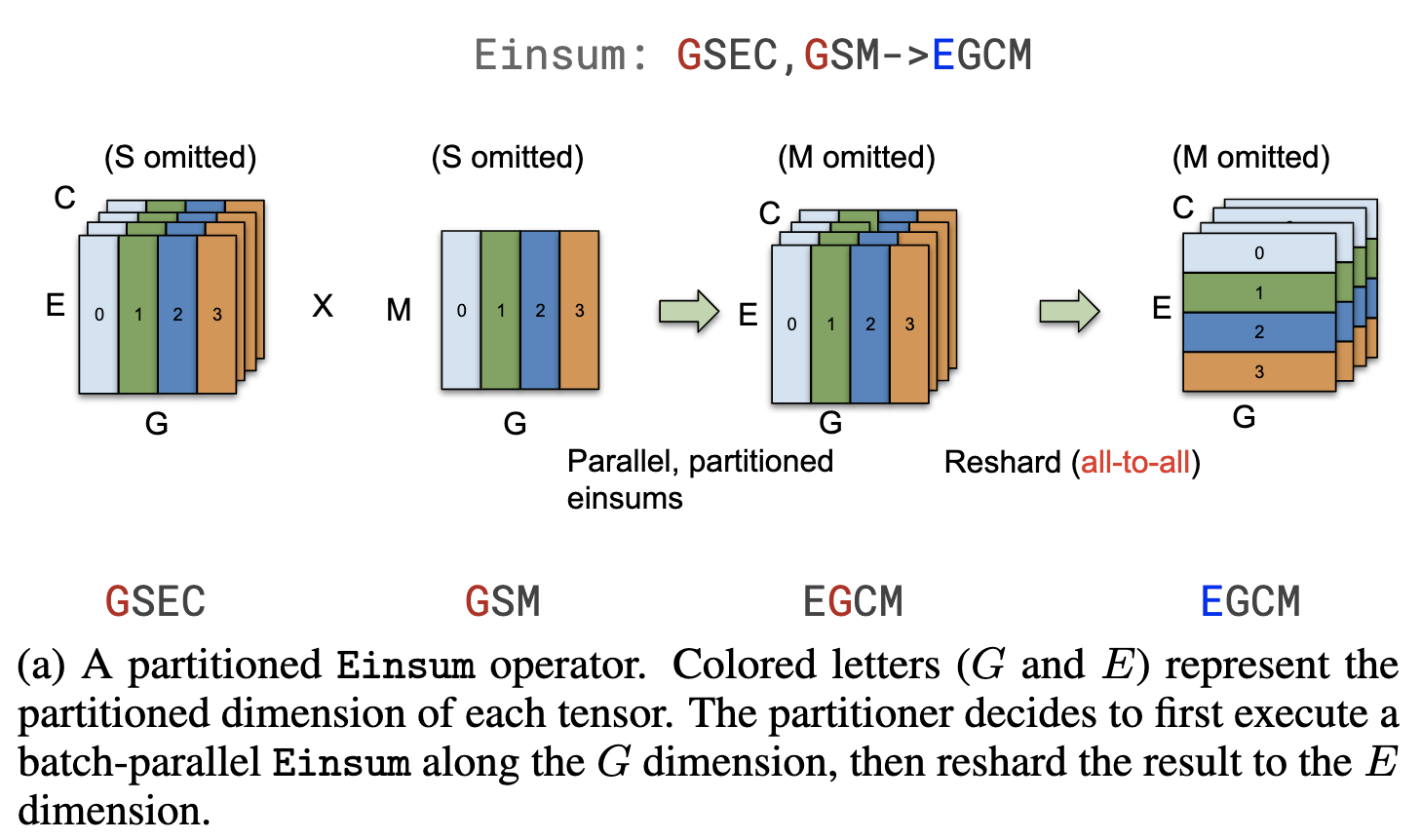
Two inputs, lhs and rhs, are tensors partitioned in the way that the figure describes. Thus, after partitioning the computation, the lhs is unwarpped, and its shape changed from f32[24, 100] to f32[24,50]. And at the end of file, AllReduce was added to collect the partial results.

upload successful
upload successful

Sharding Propagation Algorithm

The system should be able to figure out an optimal sharding specifications for the remaining tensors without user’s annotations. An ideal partitioning plan can reduce the communication amount, reduce memory footprint, and improve the performance.

upload successful
upload successful

Some unit tests written in tensorflow/compiler/xla/service/sharding_propagation_test.cc are intuitive examples.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
TEST_P(ParameterizedMetadataTest, BroadcastForwardPass) {
  const char* const hlo_string = R"(
HloModule module
ENTRY %broadcast {
  %param0 = f32[3,2048,2048]{2,1,0} parameter(0),
    sharding={devices=[1,2,2]0,1,2,3 metadata={op_name="a"}}
  %broadcast = f32[3,2048,2048,3]{3,2,1,0} broadcast(%param0), dimensions={0,1,2}
  ROOT %copy = f32[3,2048,2048,3]{3,2,1,0} copy(%broadcast)
})";
  TF_ASSERT_OK_AND_ASSIGN(auto module,
                          ParseAndReturnVerifiedModule(hlo_string));
  if (GetParam().clear_metadata) {
    ClearMetadata(module.get());
  }
  TF_ASSERT_OK_AND_ASSIGN(
      bool changed,
      ShardingPropagation(/*is_spmd=*/false, GetParam().propagate_metadata)
          .Run(module.get()));
  EXPECT_TRUE(changed);
  auto* instruction = FindInstruction(module.get(), "broadcast");
  ASSERT_NE(instruction, nullptr);
  EXPECT_THAT(instruction, op::Sharding("{devices=[1,2,2,1]0,1,2,3}"));
  if (GetParam().propagate_metadata && !GetParam().clear_metadata) {
    EXPECT_THAT(instruction->sharding(),
                ShardingMetadata({CreateMetadata("a")}));
  } else {
    EXPECT_THAT(instruction->sharding(), ShardingMetadata({}));
  }
}

It clearly shows that the system inferred the sharding specification of broadcast is {devices=[1,2,2,1]0,1,2,3}according to its input with the attribute {devices=[1,2,2]0,1,2,3}. Note that this test is called BroadcastForwardPass, there also exists a test named BroadcastBackwardPass, which is to say the propagation should be on both directions.

Reference

  • GShard: https://arxiv.org/abs/2006.16668

  • GSPMD: https://arxiv.org/abs/2105.04663

  • Julia DistributedArrays.jl: https://juliaparallel.github.io/DistributedArrays.jl/latest/index.html